Краткая биография николая лобачевского самое главное

Оглавление

Доказательства непротиворечивости геометрии Лобачевского

Не секрет, что геометрия Лобачевского не получила признания при его жизни из-за необычности. Более того, он был осмеян и к концу своих дней морально опустошен, так как считал, что теории суждено умереть вместе с создателем. Все осложнялось тем, что ученому не удалось найти объективных доказательств непротиворечивости своей теории. Для признания правоты Лобачевского потребовалось не только время, но и дальнейшее развитие математической науки, нахождение связей между различными ее разделами.

Теория Лобачевского прошла проверку временем и не оказалась пустышкой, которая, как думали его современники, в будущем сама уничтожит себя.

Фактический материал, который позволил устранить сомнения в непротиворечивости новой геометрии, был получен при разработке теории поверхностей. Если проследить за изменением свойств фигур, расположенных на изгибаемых поверхностях, то можно сделать некоторые неожиданные выводы. Сама теория поверхностей разрабатывалась немецким математиком Карлом Фридрихом Гауссом, а затем развивалась российским ученым Фердинандом Миндингом. Одним из главных понятий в теории поверхностей были так называемые геодезические линии, которые можно сравнить с обыкновенными прямыми на плоскости. И геодезические линии, и прямые выполняют одну и ту же функцию — определяют кратчайшее расстояние между точками. Разница лишь в том, что в искривленном пространстве геодезические линии представляют собой, грубо говоря, искривленные линии. Например, на сфере геодезическими линиями являются большие окружности, опоясывающие ее.

В результате Миндинг вывел формулы для геодезических треугольников (в них стороны образованы геодезическими линиями), которые совпали с планиметрией Лобачевского. Удивительно, но факт — доказательства непротиворечивости новой геометрии практически лежали на поверхности и существовали уже при жизни ученого. Однако ни один из математиков не заметил этого, так как они не были знакомы с работами друг друга. Потребовалось время, и только через 28 лет после открытия Миндинга (по прошествии 12 лет после смерти Лобачевского) итальянский геометр Эудженио Бельтрами сопоставил эти два исследования, провел строгие расчеты и вывел модель геометрии Лобачевского — три псевдосферические поверхности.

На глобусе геодезическими линиями являются долгота и широта

Таким образом и была убедительно доказана непротиворечивость, иными словами — верность геометрии Лобачевского. Она выражает свойства определенных криволинейных фигур в пространстве Евклида (таком, которое описывается аксиомами геометрии Евклида), а значит, не может быть противоречивой. Если бы она была таковой, то тогда геометрия Евклида противоречила бы сама себе, что не является истиной. Со временем было показано, что данная модель лишь частично доказывает непротиворечивость неевклидовой геометрии. Однако начало было положено.

Как только была доказана непротиворечивость геометрии Лобачевского, идеи на ее основе стали оказывать влияние на дальнейшее развитие математической науки.

Псевдосферические поверхности являются моделью геометрии Лобачевского
на плоскости

Интересно, что вскоре была опубликована переписка Гаусса, в которой фигурировало его настоящее мнение о Лобачевском, скрываемое в годы непризнания неевклидовой геометрии. Ведь симпатия к ученому и его открытию тогда грозила всеобщим осмеянием.

Полная реабилитация Лобачевского дала импульс к появлению новых моделей неевклидовой геометрии, полностью подтверждающих непротиворечивость геометрии ученого.

Александр Фридман пришел к выводу, что Вселенная расширяется с течением
времени и пространство такой Вселенной обладает геометрией Лобачевского, то есть
подчиняется законам неевклидовой геометрии

Краткая биография

1807 год – поступление в Казанский университет. В число студентов Николая Лобачевского приняли со второй попытки.
1807-1811 годы – обучение в университете. Первый курс – интерес к фармакологии и химии, затем – увлечение математикой и физикой под влиянием приглашённых из Германии профессоров Бартельса и Броннера. Участие в несанкционированных студенческих мероприятиях (маскарад, пиротехнические опыты), обеспечивших Лобачевскому репутацию вольнодумца и упрямца. Успехи в учёбе и заступничество преподавателей позволили успешно завершить обучение в 1811 году со степенью магистра по физике.
1811 год – начало совместной работы с профессором Бартельсом по изучению классических трудов Гаусса и Лапласа. Участие в наблюдениях за кометой. По результатам наблюдений написание первой научной статьи «Теория эллиптического движения небесных тел».
1813 год – получение должности адъюнкта (ассистента) чистой математики. Начало преподавательской деятельности – чтение лекций студентам по арифметике и геометрии, ведение научно-просветительской деятельности среди казанских чиновников. Публикация новых научных статей.
1816 год – избрание на должность экстраординарного профессора («профессора без должности»). Расширение списка читаемых дисциплин.
1820-26 годы – избрание на должность ординарного профессора. Работа в должности декана физико-математического факультета – активная преподавательская и организационная работа по обустройству жизни факультета. Написание учебников по алгебре и геометрии. Награждение орденом св. Владимира IV степени.
1826 год – выступление с докладом «Сжатое изложение начал геометрии», непонятым коллегами («год рождения» неевклидовой геометрии).
1827-1846 годы – деятельность в должности ректора Казанского Императорского университета: организация лабораторий, обустройство библиотеки, строительство новых корпусов, создание механических мастерских, анатомического театра, клиники и обсерватории. Установление связей Казанского университета с научными центрами Европы, направление преподавателей на стажировку. Организация этнографических экспедиций в страны Востока. Принятие, по инициативе Лобачевского, в число студентов представителей коренных народов: татар, киргизов, чувашей и др.
1832-1834 гг. – представление труда «О началах геометрии» в Академию наук (г. Санкт-Петербург), вызвавшего резкую критику и насмешки коллег. Начало издания «Учёных записок Императорского Казанского университета». Женитьба на Варваре Алексеевне Моисеевой.
1835-1838 годы – публикация статей о «Воображаемой геометрии» и «Новых начал геометрии с полной теорией параллельных», получивших высокую оценку у «короля математиков» Карла Фридриха Гаусса (Германия). В то же время острая критика работ Лобачевского на родине.
1836 год – высокая оценка деятельности Лобачевского в качестве ректора императором Николаем I, награждение орденом Анны II степени и получение права на потомственное дворянство.
1840 год – приобретение имения в 1000 гектаров в живописном месте на Волге в Чувашии. Обустройство территории: постройка дома и флигеля, разведение сада и кедровой рощи, сооружение плотины, конюшни, оранжереи и овчарни. Оценка успехов в овцеводстве на выставке в Петербурге в 1850 году (серебряная медаль).
1842 год – избрание на должность члена корреспондента ученого общества в Гёттингене (Германия).
1846-1852 годы – отстранение от должности ректора и от профессорской кафедры. Назначение помощником попечителя Казанского учебного округа.
1850-55 годы – ухудшение здоровья, финансовые трудности, повлекшие за собой разорение.
1855 год – потеря зрения.
1856 год – создание последнего труда «Пангеометрия».
1856 год – смерть (похоронен в Казани).

Портрет 1855 г.

Интересные факты из жизни Лобачевского

В гимназии увлекался пиротехническими опытами, за что попал в карцер. Его недолюбливали преподаватели за вольнодумие, упорство.
Стал магистром в 19 лет, а в 24 года – профессором.
Любил заниматься садоводчеством. Его «любимцами» в саду были кедры. Лобачевский говорил, что не дождется их плодов. Они были сняты всего через несколько месяцев после смерти ученого.
Лобачевский боялся, что его труды будут забыты после его смерти. Эти опасения подогревала интенсивная критика его работ.
В 1992 году была учреждена медаль имени Лобачевского. Ее выдают каждых пять лет за выдающиеся достижения в исследовании геометрии.
Лобачевский имел все шансы попасть в армию, когда вышел указ, предписывающий отдавать на службу тех студентов, которые отличались дурным поведением.
Во время учебы в университете нередко проявлял непочтительность к религии, что ему прощали только за блестящие познания в математике.
Активно внедрял всевозможные новшества в сельском хозяйстве. За некоторые достижения на этом поприще даже получал награды.
Владел замечательным даром убеждения. Одного своего студента, который любил выпить и даже бросался на людей с ножом, Лобачевский утихомирил лишь спокойным разговором.
Любил весело провести время со студентами, но панибратства никогда не допускал.

Значение Неевклидовой геометрии

Новая геометрия явилась чистым порождением разума, отделившейся от окружающей действительности. Поэтому Лобачевский назвал ее «воображаемой». Появление неевклидовой геометрии было важным шагом в превращении математики в науку о логически мыслимых формах и отношениях. Этот процесс шел по всему фронту не только в геометрии, но и в алгебре. Появились теория множеств, математическая логика. В геометрии вскоре за геометрией Лобачевского появилась многомерная евклидова геометрия.

Лобачевский был назван «Коперником геометрии», но его можно назвать и Колумбом науки, открывшим новую ее область, за которой следовал материк новой геометрии и вообще новой математики. Тот путь, на который впервые стал Лобачевский, в значительной степени определил лицо современной науки.

Открытие новой геометрии стало началом многочисленных исследований выдающихся математиков 19 века. Геометрия послужила толчком к развитию науки, а значит и пониманию мира, который на окружает.

А в начале 20-говека было обнаружено, что геометрия Лобачевского совершенно необходима в современной физике. Например, в теории относительности Эйнштейна, в расчетах современных синхрофазотронов, в космонавтике.

Важное замечание, касающееся чертежей, изображающих поведение прямых на плоскости Лобачевского. Как показывают опыты, наше физическое пространство по свойствам или евклидово, или очень мало от него отличается

Оперируя с чертежом, вынуждены ограничиться его малым размером, а отклонение от евклидовости, если оно существует, будет наблюдаться только при очень больших протяжениях. Поэтому для наглядности обычно принято изображать прямые, слегка их искривляя, чтобы отчётливее выразить характер их сближения или расхождения на плоскости Лобачевского. Однако Лобачевский такие вольности себе не разрешал.

Сколько времени нужно было учёным, чтобы проверить на различных моделях: псевдосфере Клейна, модель Пуанкаре, трёхмерные многообразия математика Тёрстона, что геометрия Лобачевского действует? Какие сомнения возникали у самого Лобачевского в правильности его идей?! Но именно элементы геометрии Лобачевского стали основой таких разделов математики, как теория чисел и теория функций комплексной переменной и многих других.

Геометрия Лобачевского

Разрешить проблему параллелей удалось русскому математику Николаю Ивановичу Лобачевскому. Однако доказательство было выполнено косвенно. Он просто допустил, что пятый постулат неверен, и на основании этого вывел новую (так называемую не евклидову) геометрию. Тот факт, что новая геометрия непротиворечива, удалось доказать лишь спустя тридцать лет. Отсюда следует, что проблема параллелей снимается сама собой.

«Непересекаемость» бесконечно длинных параллельных прямых кажется для нас
очевидной, однако доказать справедливость этого утверждения напрямую невозможно

Лобачевский вместо пятого постулата сформулировал новую аксиому параллельных прямых, которая по смыслу оказалась прямо противоположна пятому постулату Евклида:

Через точку вне прямой можно провести не одну прямую, не встречающуюся с данной прямой, а по крайней мере две.

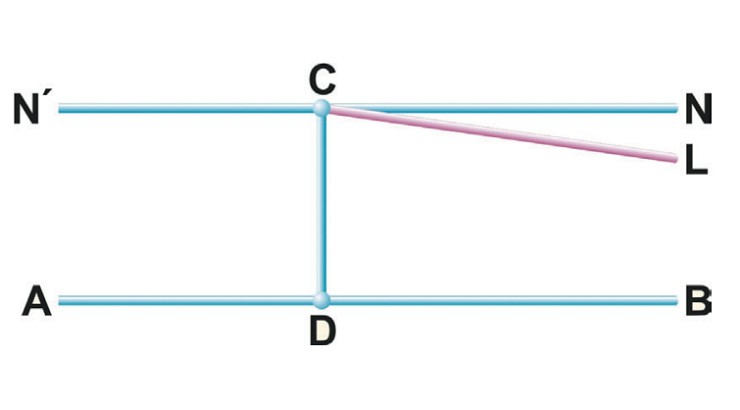Если из точки С, расположенной вне прямой AB, опустить на прямую AB
перпендикуляр СD, а затем еще к прямой CD построить перпендикуляр CN, то легко
доказывается, что NN (прямая, полученная продолжением CN) будет параллельна
прямой AB. Из пятого постулата Евклида следует, что из всех прямых плоскости ABC,
которые проходят через точку С, только одна прямая NN не будет встречаться с прямой
AB. Нам кажется это очевидным! Однако Лобачевский отказался от этого утверждения
и допустил, что через точку С проходит по крайней мере еще одна прямая (например,
CL), которая тоже не пересекает AB

На основании этой теоремы и остальных четырех постулатов абсолютной геометрии Лобачевский и получил свою, которая была так же логически безупречна, как и геометрия Евклида.

Аксиома Лобачевского на первый взгляд может показаться абсурдной или как минимум странной. Кажется, что он подменяет очевидное неочевидным, противоречит установившимся геометрическим представлениям. Но если этот вопрос рассмотреть глубже, то неочевидность именно пятого постулата Евклида будет налицо.

Так, если внимательно прочитать первые четыре постулата Евклида, можно заметить, что они относятся к фигурам ограниченного размера, а пятый — нет. Он оперирует неограниченной, бесконечной прямой. В итоге если мы захотим проверить правильность данного постулата на практике, то не сможем это сделать, поскольку такой эксперимент осуществить невозможно. Можно представить следующую ситуацию. Например, если предположить, что угол MCL очень маленький, а затем продлить отрезки CL и AB, то, даже обладая необширной фантазией, можно представить, что при таких условиях эти прямые не пересекутся даже на расстоянии, выходящем за пределы нашей планеты! В то же время если взять какую-либо ограниченную часть пространства, например круг, то каким бы большим он ни был, мы можем провести множество прямых, проходящих через точку С и не пересекающих прямую AB.

Первая страница сочинения Н. И. Лобачевского «О началах геометрии» (1829–
1830). Первое опубликованное исследование в области неевклидовой геометрии
не было признано Российской Академией наук. «Автор, по-видимому, задался целью
писать таким образом, чтобы его нельзя было понять», — так написал в рапорте
известный математик и академик М. В. Остроградский

Поэтому нет никаких оснований считать утверждение Лобачевского неправильным.

Отличие двух противоположных по своей сути предположений заключается только в том, что евклидов постулат более понятен человеческому сознанию.

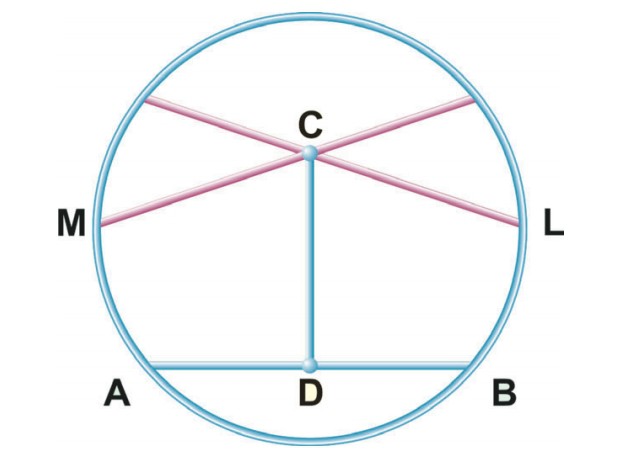В ограниченном пространстве (круге) через точку С можно провести более одной
прямой (CL и CM), не пересекающей прямую AB

Он соответствует нашему обыденному восприятию, в конце концов мы к нему привыкли… В этом случае можно вспомнить, что у древних было распространено представление, будто Земля плоская, а факт, что она круглая (как предполагала революционная гелиоцентрическая теория Коперника), полностью отрицался. Однако в отличие от теории Коперника, в которой говорилось об ином расположении и движении тел в пространстве, понимание идеи Лобачевского требует более абстрактного мышления.

Неудивительно, что свою геометрию Лобачевский назвал воображаемой, а Евклидову — употребительной, что подчеркивало ее более естественные основы. Более того, в поздних трудах для своей новой теории ученый применял термин «пангеометрия» (всеобщая геометрия). Такое название подчеркивало, что геометрия Евклида — всего лишь частный (предельный) случай геометрии Лобачевского.

Лобачевский: биография и открытия кратко

Н. И. Лобачевский

Николай Иванович Лобачевский, великий российский математик, получил всемирную известность как автор неевклидовой геометрии.

Служил преподавателем, деканом и ректором в знаменитом на всю Россию Казанском университете.

Н.И. Лобачевский (годы жизни 1792-1856)

Н.И. Лобачевский появился на свет в Нижнем Новгороде в конце 1792 г. в небогатой семье провинциального чиновника. В 1800 году отец умирает, и вдова с сыном переезжает в Казань.

С 1802 по 1806 год Коля учился в гимназии. Затем поступил в Казанский университет. В то время курс математики читал близкий друг Гаусса — М.Ф. Бартельс, сразу заметивший выдающиеся способности бедного студента и взявший его под свою опеку.
В 1811 г., получив красный диплом и защитив степень магистра, юный Лобачевский получает остается работать в университете. Спустя несколько месяцев им был представлен научному сообществу первый труд — “Теория эллиптического движения небесных тел”, а через два года второй – “О разрешении алгебраического уравнения”.
Спустя три года ученый занял должность адъюнкта, затем — профессора. Он читает лекции по математике, астрономии, физике. В 1819 г. избран деканом факультета физики и математики, затем, в период 1827-1846 гг., служил ректором, не прекращая научную работу.
Весной 1819 г. в университет прибывает ревизор — М.Л. Магницкий, признавший весьма плачевным состояние дел в вузе и вынудивший Лобачевского подать в отставку. Здоровье Лобачевского резко ухудшилось, как и его финансовое состояние, он был вынужден продать все свое имущество.
В 1832 году Николай Иванович женился, его супруга Варвара Моисеева родила 18 детей, большинство из которых умерло во младенчестве, выжили лишь семеро. В 1852 г. умирает старший сын ученого, эта потеря усугубила и без того плохое состояние здоровье ученого, у него резко ухудшилось зрение. Но и ослепнув, он посещал экзамены и торжества в университете, принимал участие в ученых диспутах, работал над своими трудами. Его главную работу «Пангеометрия» записывали студенты под диктовку.

Умер великий математик в феврале 1856 г., спустя 30 лет после первого опубликования его теории неевклидовой геометрии. Могила находится в Казани, на Арском кладбище.

После смерти имя великого математика было увековечено в названиях улиц и библиотек, одного из лунных кратеров.

В 1895 году было принято решение об учреждении премии Лобачевского, которая вручалась вместе с одноименной медалью.

Вклад Лобачевского в науку

Как считал ученый, аксиома параллельности, выдвинутая Евклидом, была жестким произвольным ограничением, и он выдвинул свою аксиому о прохождении множества параллельных прямых через не находящуюся на прямой точку.

Свое открытие Николай Иванович обнародовал в 1826 году, затем написал еще несколько работ по этой тематике.

Научное сообщество России не приняло идеи Лобачевского, и ученый в 1837 г. публикует в Германии труд “Воображаемая геометрия”.

Великий математик Гаусс продвигает заинтересовавшие его идеи русского математика. Чтобы ознакомиться с оригинальным текстом, он начал учить русский язык.

Гаусс рекомендует избрать русского математика членом-корреспондентом Геттингенского королевского общества, и в 1842 г. это событие произошло.

На счету у Лобачевского и другие открытия. Им были разработаны:

способ приближенного решения уравнений;
ряд теорем, касающихся тригонометрических рядов;
понятие о признаке сходимости рядов:
понятие о непрерывной функции;
способ численного решения уравнений.

Ученый, опередивший современников на десятки лет, не был по достоинству оценен ими.

Написанные им 2 учебника по алгебре и геометрии для гимназистов остались непризнанными. Кардинально пересмотрев понятия эпохи Евклида, он открыл новую геометрию.

Но составленный им доклад о геометрических началах не получил вообще никакой оценки от именитых профессоров, а сама рукопись затерялась.

В 1930 году журнал “Казанский вестник” публикует работу ученого “О началах геометрии”.

В ней были изложены важные геометрические открытия, а также дано описание уточненного определения функции.

Наследие Лобачевского

Занимая должность ректора Казанского университета, Лобачевский повысил уровень научно-учебной деятельности учебного заведения, под его руководством было построено множество служебных зданий, был основан научный журнал. Именно благодаря Лобачевскому университет в Казани считался одним из лучших.

К сожалению, его научные идеи противоречили общепринятым аксиомам. Несмотря на это, он в 1835-1839 г. г. печатает свои труды “Воображаемая геометрия”, “Применение воображаемой геометрии к некоторым интегралам”, “Новые начала геометрии с полной теорией параллельных”.

Карьера

Главное достижение Лобачевского — это развитие (независимо от Яноша Бойяи ) неевклидовой геометрии , также называемой геометрией Лобачевского. Перед ним, математики пытались вывести Евклид «S пятый постулат из других аксиом . Пятое правило Евклида — это правило евклидовой геометрии, которое гласит (в переформулировке Джона Плейфэра ), что для любой данной линии и точки не на прямой, есть только одна линия, проходящая через точку, не пересекающую данную линию. Вместо этого Лобачевский разработал геометрию, в которой пятый постулат не соответствовал действительности. Эта идея была впервые сообщили 23 февраля (11 февраля, OS ), 1826 на заседание кафедры физики и математики, и это исследование было напечатано О происхождении геометрии ( О началах геометрии ) в 1829-1830 (Казань Примечания к университетскому курсу). В 1829 году Лобачевский написал статью о своих идеях под названием «Краткое изложение основ геометрии», которая была опубликована « Казанским вестником», но была отклонена при передаче в Петербургскую Академию наук для публикации.

Неевклидова геометрия, разработанная Лобачевским, называется гиперболической геометрией . Лобачевский заменил аксиому Playfair утверждением, что для любой данной точки существует более одной линии, которая может быть продолжена через эту точку и параллельна другой линии, частью которой эта точка не является. Он разработал угол параллельности, который зависит от расстояния точки от заданной линии. В гиперболической геометрии сумма углов в гиперболическом треугольнике должна быть меньше 180 градусов. Неевклидова геометрия стимулировала развитие дифференциальной геометрии, имеющей множество приложений. Гиперболическую геометрию часто называют «геометрией Лобачевского» или «геометрией Бояи – Лобачевского».

Некоторые математики и историки ошибочно утверждали, что Лобачевский в своих исследованиях неевклидовой геометрии находился под влиянием Гаусса, что неверно. Сам Гаусс очень высоко ценил опубликованные работы Лобачевского, но между ними никогда не было личной переписки до публикации. Хотя трем людям — Гауссу, Лобачевскому и Бойяи — можно приписать открытие гиперболической геометрии, Гаусс никогда не публиковал свои идеи, а Лобачевский был первым, кто представил свои взгляды мировому математическому сообществу.

«Magnum opus Geometriya» Лобачевского был завершен в 1823 году, но не был опубликован в его точном первоначальном виде до 1909 года, спустя много времени после его смерти. Лобачевский был также автором « Новых основ геометрии» (1835–1838). Он также написал « Геометрические исследования по теории параллелей» (1840 г.) и пангеометрии (1855 г.).

Еще достижений Лобачевского разрабатывает метод для приближения из корней в алгебраических уравнений . Этот метод теперь известен как метод Данделина – Греффе в честь двух других математиков, которые открыли его независимо. В России это называется методом Лобачевского. Лобачевский дал определение функции как соответствие между двумя наборами действительных чисел ( Питер Густав Лежен Дирихле дал такое же определение независимо вскоре после Лобачевского).

Начало научной деятельности

По протекции знакомых ученых Броннера и Бартельса весной 1814 года Лобачевский становится адъюнктом (доцентом) чистой математики. Еще через два года его утверждают экстраординарным профессором. На протяжении 5 лет ученый занимался преподаванием исключительно математических дисциплин, таких как алгебра, тригонометрия, плоская и сферическая геометрия, курсы высшей математики.

Лобачевский предположил, что в трехмерном пространстве параллельные прямые вполне могут иметь общие точки

В 1819 году получает должность декана физико-математического факультета Казанского университета. За несколько лет Лобачевский пишет и издает несколько учебников. Первый по геометрии был осужден современниками через чрезмерный отход от Евклидовых канонов, из-за чего и не был издан при жизни автора. Второй учебник по алгебре автор смог издать только спустя 10 лет (в 1834 году).

В 1827 году получает самую ответственную в своей жизни должность – ректора университета. Он сразу берется за реорганизацию штата и структуры университета в целом. За время его руководства построено несколько новых корпусов, лабораторий, поддерживалось развитие библиотеки, издание «Казанского Вестника», «Ученых записок Казанского университета». По его инициативе в учебном заведении появился большой кабинет физики и астрономическая обсерватория.

Неевклидова геометрия

Величайшим РЅР°СѓС‡РЅС‹Рј подвигом Николая Лобачевского считается создание им первой неевклидовой геометрии, историю которой принято отсчитывать от заседания Отделения физико-математических наук в Казанском университете 11 С„РµРІСЂР°Р»СЏ 1826, на котором Лобачевский выступил с докладом «Сжатое изложение основ геометрии со строгим доказательством теоремы о параллельных». В протоколе заседания об этом великом событии следующая запись: «Слушано было представление Г. Орд. Профессора Лобачевского от 6 С„РµРІСЂР°Р»СЏ сего года с приложением своего сочинения на С„СЂР°РЅС†СѓР·СЃРєРѕРј, о котором он желает знать мнение членов Отделения и, ежели оно будет выгодно, то просит сочинение принять в составление ученых записок Физико-математического факультета».

В 1835 году Н. Лобачевский кратко сформулировал побудительные мотивы, которые привели его к открытию неевклидовой геометрии: «Напрасное старание со времен Евклида в продолжении двух тысяч лет заставило меня подозревать, что в самих понятиях еще не заключается той истины, которую хотели доказать и которую проверить, подобно другим физическим законам, могут лишь опыты, каковы, например, астрономические наблюдения. В справедливости моей догадки будучи наконец убежден и почитая затруднительный вопрос решенным вполне, писал об этом я рассуждение в 1826 году».

Лобачевский исходил из допущения, согласно которому через точку, лежащую вне данной прямой, проходит несколько прямых, не пересекающихся с данной прямой. Развивая следствия, проистекающие из этого допущения, которое противоречит знаменитому V постулату (в других вариантах 11-ой аксиоме) «Начал» Евклида, Лобачевский не убоялся сделать дерзкий шаг, перед которым из опасения противоречий останавливались его предшественники: построить геометрию, противоречащую повседневному опыту и «здравому смыслу» — квинтэссенции повседневного опыта.

Ни комиссия в составе профессоров И. М. Симонова, А. Я. Купфера и адъюнкта Н. Д. Брашмана, назначенная для рассмотрения «Сжатого изложения», ни другие современники Лобачевского,в том числе выдающийся математик Рњ. Р’. РћСЃС‚СЂРѕРіСЂР°РґСЃРєРёР№, не смогли по достоинству оценить открытие Лобачевского. Признание пришло лишь через 12 лет после его кончины, когда в 1868 г. Э. Бельтрами показал, что геометрия Лобаческого может быть реализована на псевдосферических поверхностях в евклидовом пространстве, если за прямые принять геодезические.

К неевклидовой геометрии пришел также Янош Бойяи, но в менее полной форме и на 3 года позже (1832).

литература

Б.А. Розенфельд : Лобачевский Николай Иванович . В: Чарльз Коулстон Гиллиспи (ред.): Словарь научной биографии . лента8 : Джонатан Гомер Лейн — Пьер Жозеф Макер . Сыновья Чарльза Скрибнера, Нью-Йорк, 1973, стр.428-435 .
Д.А. Гудков : Н.И. Лобачевский, Нижний Новгород, 1992.
Вениамин Федорович Каган: Н. Лобачевский, Москва, Ленинград 1948 (русский, французский перевод Москва 1974)
А.В. Васильев: Николай Иванович Лобачевский: 1792–1856, Москва: Наука, 1992.
Г. Касдорф: Лобачевский, в H. Wussing, W. Arnold, биографии выдающихся математиков, Берлин, 1983
Александр Петрович Норден , А.П. Широков: Наследие Н.И. Лобачевского и деятельность казанских геометров, Российские математические исследования, Том 48, 1993, стр. 47-74.
А. Вучинич: Николай Иванович Лобачевский: Человек, стоящий за первой неевклидовой геометрией, Исида, Том 53, 1962, стр. 465-481.

Список литературы

1. Лаптев Б.Л., Великий русский математик, «Вестник высшей школы», 1967, № 12 — с. 8-11;

2. Лобачевский Н.И., Сочинения по геометрии, М. — Л., 1946 — 49 (Полн. собр. соч., т. 1 — 3) — с. 59, 72-78 ;

3. Элементарное доказательство непротиворечивости планиметрии Лобачевского, М., 1956- с. 7-19;

4. Каган В.Ф. Геометрия Лобачевского и ее предистория, М. — Л., 1949 (Основания геометрии, ч. 1) — с. 142-158;

5. В.С. Антонов «Энциклопедия по истории России XIX века».

6. А.М. Прохоров «Энциклопедический словарь» — с. 163-167.

7. Лаптев В.И. Жизнь и деятельность Н.И. Лобачевского // Успехи математических наук. — М., 1951. — Т. 6. — № 3 (43). — с. 10-17.

Неевклидова геометрия Лобачевского (adsbygoogle = window.adsbygoogle || []).push({});

Колоссальное число текущих дел, широкая педагогическая, административная и исследовательская работа не стали препятствием для творческой деятельности математика: из-под его пера вышли 2 учебника для гимназий — «Алгебра» (осужденная за применение метрической системы мер) и «Геометрия» (вовсе не опубликованная). Со стороны Магницкого за Николаем Ивановичем был установлен строгий надзор, по причине проявления ним дерзости и нарушения установленных инструкций. Однако и в этих условиях, действующих унизительно на человеческое достоинство, Лобачевский Николай Иванович упорно трудился над строгим построением геометрических основ. Результатом столь кропотливого труда стало открытие ученым новой геометрии, совершенное на путях кардинального пересмотра понятий эпохи Евклида (ІІІ век до н. э.).

Зимой 1826 года русским математиком был осуществлен доклад о геометрических началах, переданный на отзыв нескольким именитым профессорам. Однако ожидаемой рецензии (ни положительной, ни даже отрицательной) не поступило, а рукопись ценного доклада до наших времен не дошла. Данный материал ученый включил в свой первый труд «О началах геометрии», напечатанный в 1829-1830 гг. в «Казанском вестнике». Помимо изложения важных геометрических открытий, Николай Иванович Лобачевский описал уточненное определение функции (четко разграничивая ее непрерывность и дифференцируемость), незаслуженно приписанное немецкому математику Дирихле. Также ученым были сделаны тщательные исследования тригонометрических рядов, оцененные несколько десятилетий спустя. Талантливый математик является автором метода численного решения уравнений, со временем несправедливо получившего название «метод Греффе».

Время перемен

Однако очень скоро эта активная деятельность прервалась. В 1819 году императором Александром I был назначен куратором Казанского академического округа Михаил Магнитский. Его доклад шокировал — он обвинил персонал в том, что тот тратит деньги правительства и ликвидирует религиозный аспект образования. Магнитский даже предложил снести само здание, в котором размещался университет. Эта решительная мера не была поддержана ни императором, ни окружным советом по образованию. Вместо этого они предложили реструктурировать университет и наблюдать Магнитскому за изменениями.

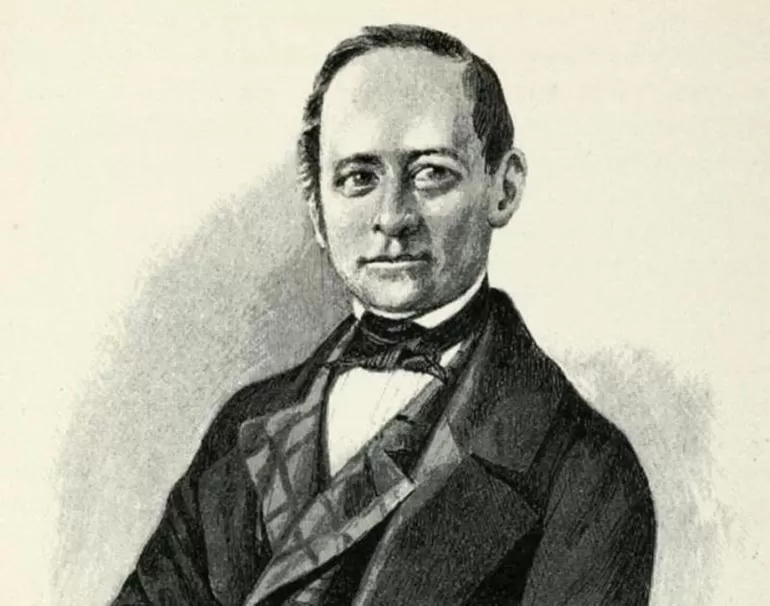
Суть реформирования, по мнению Магнитского, сводилась к двум вещам — устранению свободного мышления и привлечению религиозного образования. Университет потерял свою независимость и вскоре напоминал монастырь, а не учебное заведение. Магнитский уволил 11 профессоров и всех, кто не был согласен с его мнением. Что касается студентов, то их жизнь стала ещё более несчастной — в соответствии с новой идеологией, «суть обучения заключалась в повиновении». Они помещались в «комнаты подчинения» за малейшее нарушение правил и недовольные высказывания, а их рацион уменьшен до хлеба и воды.

Лобачевский, ставший профессором в 1822 году, был потрясён изменениями в его альма-матер. Человек, который попал в беду из-за свободомыслия, будучи студентом, теперь оказался в сложном положении как профессор — его критика новых правил поставила его на грань увольнения. В своём докладе ректору университета Магнитский писал: «Не проходит и года без того, чтобы профессор Лобачевский не пытался умышленно нарушить наши инструкции. За ним нужно внимательно следить».

Нет никаких сомнений в том, что Лобачевский потерял бы свою работу, но в конце 1825 года от брюшного тифа умер император Александр I. Весной следующего года новый император Николай I направил независимую инспекционную комиссию в университет. По прибытии инспекторы стали свидетелями полного разрушения школы и огромного хищения государственных средств. Магнитский был уволен, а его имущество конфисковано, чтобы компенсировать кражу.

Научные открытия

Слава пришла к Лобачевскому, когда он стал ректором Казанского университета. До него учебным заведением управлял Магнитский, и это привело к серьезному упадку. Николай Иванович восстановил университет.

Лобачевский сумел опровергнуть пятый постулат Евклидовой геометрии. В 1826 году он предоставил свои размышления в виде доклада, но они не получили должного интереса со стороны научного общества. Математик попробовал опубликовать свои работы, но безуспешно.

Неевклидовой геометрией заинтересовался Гаусс. Он тоже учился у Бартельса, неудивительно, что у него были такие же теории, как и у Лобачевского. Гаусс признавал заслуги русского математика.

К достижениям Лобачевского можно отнести:

Разработал метод решения приближенного решения уравнений.
Создал теоремы о тригонометрических рядах.
Уточнил понятие непрерывной функции.